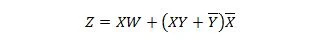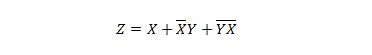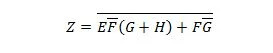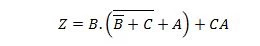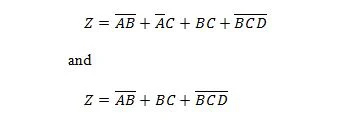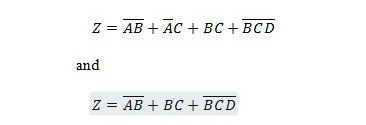Κεφάλαιο 2: Boolean Algebra and Its Related Components Computer
2.1 Βασικοί τελεστές Boolean
Ας υποθέσουμε ότι εγώ (ο συγγραφέας) είμαι ψηλός και εσύ (ο αναγνώστης) είσαι ψηλός. Εάν κάποιος σας ρωτήσει αν είμαστε και οι δύο ψηλοί, θα λέγατε «Ναι» (αλήθεια). Αν ρωτήσει αν είμαστε και οι δύο κοντοί, θα λέγατε «Όχι» (ψευδή). Αν είσαι κοντός και εγώ ψηλός και σε ρωτάει αν είσαι ψηλός είτε εσύ είτε εγώ, η απάντησή σου θα ήταν «Ναι» (αλήθεια). Αν ρωτήσει αν και εσείς και εγώ είμαστε ψηλοί, δεν θα είχατε απάντηση. Μπορείτε να συνεχίσετε λέγοντας ότι η τελευταία ερώτηση δεν πρέπει να τεθεί ή ότι η ερώτηση δεν έχει απάντηση. Λοιπόν, θέλω να ξέρεις (ο αναγνώστης) ότι σήμερα, υπό ορισμένες συνθήκες, πρέπει να τεθεί το ερώτημα.
Στη βιολογία, ένα άτομο είναι είτε ψηλό είτε κοντό. Είναι οι «περιβαλλοντικές» συνθήκες που κάνουν το άτομο να έχει μέτριο ύψος. Ένας επιστήμονας, ο George Boole, όρισε ένα σύνολο απαντήσεων ή κανόνων για αυτού του είδους τις ερωτήσεις. Θα μάθουμε αυτούς τους κανόνες σε αυτήν την ενότητα του διαδικτυακού μαθήματος καριέρας (κεφάλαιο). Αυτοί οι κανόνες χρησιμοποιούνται σήμερα στους υπολογιστές, στον προγραμματισμό, στα ηλεκτρονικά και στις τηλεπικοινωνίες. Στην πραγματικότητα, χωρίς αυτούς τους κανόνες, δεν θα είχατε υπολογιστή, όπως συνηθίζεται σήμερα. δεν θα είχατε επίσης προγραμματισμό, όπως συνηθίζεται σήμερα.
Σωστό ή λάθος
Μια απλή δήλωση ανθρώπινης γλώσσας είναι είτε αληθινή είτε ψευδής από μόνη της. Αν πω, 'Είμαι ψηλός', αυτό είναι είτε αλήθεια είτε λάθος. Αν πω, «είσαι ψηλός», αυτό είναι είτε αλήθεια είτε λάθος. Αν είμαι ψηλός κι εσύ κοντός, και τίθεται η ερώτηση αν και εσύ και εγώ είμαστε ψηλοί, στη Λογική Boolean, πρέπει να δοθεί απάντηση αλήθειας ή ψευδούς. Ποιο από αυτά τα δύο πρέπει να δοθεί; Ο Boole δεν απάντησε πραγματικά σε αυτήν την ερώτηση. Απλώς κατέληξε σε ένα σύνολο κανόνων που πρέπει να ακολουθήσουμε. Τα καλά νέα είναι ότι, όταν ακολουθείτε αυτούς τους κανόνες στο σωστό πλαίσιο, δεν έχετε καμία ασάφεια. Χάρη σε αυτούς τους κανόνες, έχουμε υπολογιστές και προγραμματισμό σήμερα. Οι κανόνες σας δίνονται τώρα. Οι κανόνες δεν μπορούν πραγματικά να εξηγηθούν. απλά τους αποδέχεσαι. Οι κανόνες είναι κάτω από τρεις επικεφαλίδες: ΚΑΙ, Ή, και ΟΧΙ.
ΚΑΙ
Η ερώτηση μπορεί να τεθεί εάν και εσείς και εγώ είμαστε ψηλοί. Στη συνέχεια, το ύψος μου και το ύψος σας συνδυάζονται με το σύνολο κανόνων ΚΑΙ. Αυτοί είναι οι κανόνες ΚΑΙ που πρέπει να ακολουθήσετε:
ψευδής ΚΑΙ ψευδής = ψευδής
ψευδής ΚΑΙ αληθής = ψευδής
αληθής ΚΑΙ ψευδής = ψευδής
αληθινό ΚΑΙ αληθινό = αληθινό
Τώρα, ας είναι το ψηλό αληθές και το κοντό ψεύτικο. Αυτό σημαίνει ότι αν είμαι κοντός ΚΑΙ εσύ είσαι κοντός, εσύ κι εγώ είμαστε κοντοί. Αν είμαι κοντός ΚΑΙ είσαι ψηλός, εσύ κι εγώ είμαστε κοντοί. αυτή είναι η Boolean απάντηση που πρέπει να αποδεχτείτε. Αν είμαι ψηλός ΚΑΙ εσύ είσαι κοντός, και εσύ και εγώ είμαστε κοντοί. Αν είμαι ψηλός ΚΑΙ είσαι ψηλός, εσύ κι εγώ είμαστε ψηλοί. Όλα αυτά είναι ΚΑΙ Boolean κανόνες που εσείς (ο αναγνώστης) πρέπει απλώς να αποδεχτείτε.
Ή
Η ερώτηση μπορεί να τεθεί εάν εσείς Ή εγώ είναι ψηλός. Το ύψος μου και το ύψος σας συνδυάζονται στη συνέχεια με το σύνολο κανόνων OR. Αυτοί είναι οι κανόνες OR που πρέπει να ακολουθήσετε:
ψευδής Ή ψευδής = ψευδής
false OR true = true
αληθινό Ή ψευδές = αληθές
αληθινό Ή αληθινό = αληθινό
Και πάλι, αφήστε το ψηλό να είναι αληθινό και το κοντό ψεύτικο. Αυτό σημαίνει ότι αν είμαι κοντός Ή είσαι κοντός, εσύ Ή εγώ είναι κοντός. Αν είμαι κοντός Ή είσαι ψηλός, εσύ ή εγώ είναι ψηλός. Αν είμαι ψηλός Ή είσαι κοντός, εσύ Ή εγώ είσαι ψηλός. Αν είμαι ψηλός Ή είσαι ψηλός, εσύ ή εγώ είναι ψηλός. Όλα αυτά είναι Boolean κανόνες που πρέπει να αποδεχτείτε.
ΔΕΝ
Τώρα, στη λογική Boolean, υπάρχουν μόνο δύο καταστάσεις (πιθανές απαντήσεις). Δηλαδή αν ΔΕΝ είσαι ψηλός είσαι κοντός. Αν ΔΕΝ είσαι κοντός, είσαι ψηλός. τίποτα άλλο. Αυτοί είναι οι κανόνες που ΔΕΝ πρέπει να ακολουθήσετε:
ΟΧΙ ψευδές = αληθές
ΟΧΙ αληθές = ψευδές
Ας υποθέσουμε ότι έχετε μια χορδή (ή ελατήριο) που μπορείτε να επεκτείνετε (τραβήξετε). Ενώ η χορδή είναι στη φυσική της κατάσταση, αν πω, 'ΟΧΙ σύντομη', θα την επεκτείνετε. αυτή είναι η ερμηνεία. Ενώ η συμβολοσειρά είναι εκτεταμένη, αν πω, 'ΟΧΙ μεγάλη', θα της επιτρέψετε να συστέλλεται. αυτή είναι η ερμηνεία.
Πρέπει να απομνημονεύσετε όλους τους κανόνες στις διάφορες κατηγορίες τους.
Περισσότεροι από δύο τελεστές
Σε μια γλώσσα υπολογιστή, τα AND, OR και NOT ονομάζονται το καθένα τελεστής. Για τον τελεστή NOT, χρειάζεστε μόνο έναν τελεστή (τιμή για έναν τελεστή) για να έχετε μια απάντηση. Για τους τελεστές AND ή OR, μπορείτε να έχετε περισσότερους από δύο τελεστές. Οι προηγούμενες περιπτώσεις δείχνουν δύο τελεστές για AND και OR. Μπορείτε να έχετε τρεις τελεστές για το AND ως εξής:
ψευδής ΚΑΙ ψευδής ΚΑΙ ψευδής = ψευδής
ψευδής ΚΑΙ ψευδής ΚΑΙ αληθής = ψευδής
Αυτές είναι δύο γραμμές. το καθένα έχει δύο τελεστές ΚΑΙ. Στην πραγματικότητα υπάρχουν εννέα γραμμές όταν οι τελεστές είναι τρεις. Με τον τελεστή AND, μόνο η τελευταία γραμμή (ένατη γραμμή) είναι ίση με true. όλες οι προηγούμενες γραμμές είναι ψευδείς. Σημειώστε ότι με δύο τελεστές για AND, μόνο η τελευταία γραμμή είναι αληθινή ακόμα. και οι τρεις προηγούμενες γραμμές είναι ψευδείς. Όταν οι τελεστές είναι τέσσερις, υπάρχουν 16 γραμμές και μόνο η τελευταία γραμμή ισχύει για τον τελεστή AND.
Το μοτίβο για AND και το μοτίβο για OR είναι διαφορετικά. Με τρεις τελεστές για δύο τελεστές OR, υπάρχουν επίσης εννέα γραμμές και μόνο η πρώτη γραμμή, αυτή τη φορά, είναι ψευδής. Η δεύτερη έως την ένατη γραμμή είναι αλήθεια. Σημειώστε ότι με δύο τελεστές για OR, μόνο η πρώτη γραμμή είναι αληθινή ακόμα. και οι υπόλοιπες τρεις γραμμές είναι ψευδείς. Όταν οι τελεστές είναι τέσσερις για το OR, υπάρχουν επίσης 16 γραμμές.
Ο τελεστής NOT ασχολείται μόνο με έναν τελεστή. Το NOT false είναι αληθινό και το NOT true είναι ψευδές.
2.2 Πίνακας αλήθειας δύο τελεστών και τα ηλεκτρονικά τους στοιχεία
Στα μαθηματικά, υπάρχει ένα θέμα που ονομάζεται άλγεβρα. Ένα μικρό μέρος του φάνηκε στο προηγούμενο κεφάλαιο. Υπάρχει ένα είδος άλγεβρας που ονομάζεται άλγεβρα Boole. Στην άλγεβρα Boole, το true προσδιορίζεται από το βασικό δύο ψηφίο που είναι 1 και το false προσδιορίζεται από το βασικό δύο ψηφίο που είναι 0.
Τα εξαρτήματα της εσωτερικής μονάδας υπολογιστή είναι ηλεκτρονικά εξαρτήματα. Η μονάδα συστήματος του συστήματος υπολογιστή έχει ψηφιακά ηλεκτρονικά εξαρτήματα. Η λειτουργία AND γίνεται από ένα μικρό ηλεκτρονικό εξάρτημα που ονομάζεται πύλη AND. Η λειτουργία OR γίνεται από το μικρό ηλεκτρονικό εξάρτημα που ονομάζεται πύλη OR. Η λειτουργία NOT γίνεται από το μικρό ηλεκτρονικό εξάρτημα που ονομάζεται πύλη NOT. Πάρα πολλές από αυτές τις πύλες μπορεί να βρίσκονται σε τσιπ ολοκληρωμένου κυκλώματος (IC).
AND Truth Table and Its Gate
Ο παρακάτω πίνακας δίνει τον πίνακα αλήθειας ΚΑΙ και το σύμβολο του AND πύλη (μικρό κύκλωμα):
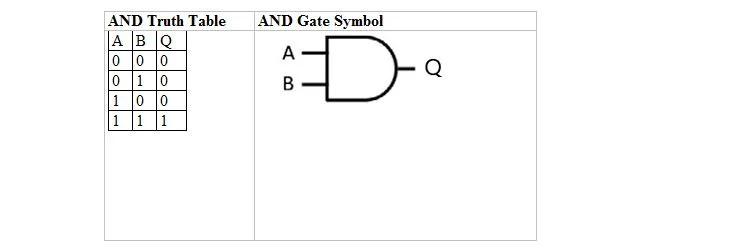
Τόσο για τον πίνακα αλήθειας AND όσο και για την πύλη του, το A και το B είναι δύο μεταβλητές εισόδου. Q είναι η μεταβλητή εξόδου. Το A είναι είτε 1 είτε 0. Το B είναι είτε 1 είτε 0. Το Q είναι είτε 1 είτε 0. Ο πίνακας AND με 1 και 0 είναι ίδιος με την προηγούμενη διάταξη true/false ΚΑΙ αλήθεια (πίνακας). Η εξίσωση ΚΑΙ είναι:
ΕΝΑ . B = Q
όπου η τελεία (.) σημαίνει ΚΑΙ (Boolean). Η τελεία μπορεί να παραλειφθεί για να έχει AB = Q που σημαίνει το ίδιο πράγμα (ΚΑΙ).
Σημείωση: Τα bit για το Α και το Β στις τέσσερις σειρές, ως ζεύγη, είναι οι τέσσερις πρώτοι αριθμοί στη βάση δύο που ξεκινούν από το 0 (ή το 00), δηλαδή 00, 01, 10, 11.
Ο παρακάτω πίνακας δίνει τον πίνακα αλήθειας OR και το σύμβολο της πύλης OR (μικρό κύκλωμα):
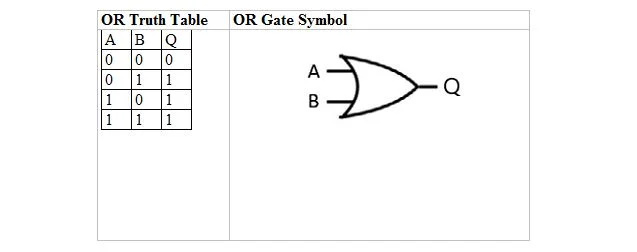
Τόσο για τον πίνακα αλήθειας OR όσο και για την πύλη του, το A και το B είναι δύο μεταβλητές εισόδου. Q είναι η μεταβλητή εξόδου. Ο πίνακας αλήθειας OR με 1 και 0 είναι ο ίδιος με την προηγούμενη διάταξη αλήθειας ή αλήθειας (πίνακας).
Η εξίσωση OR είναι:
A + B = Q
Όπου το + εδώ σημαίνει Boolean OR και όχι πρόσθεση. Η εξίσωση διαβάζεται ως 'A ή B ίσο Q'.
Ο παρακάτω πίνακας δίνει τον πίνακα NOT αλήθειας και το σύμβολο του NOT gate (μικρό κύκλωμα):
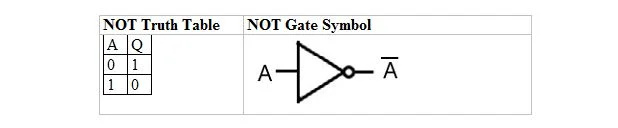
Ο πίνακας NOT αλήθειας ή η πύλη NOT έχει μόνο μία είσοδο και μία έξοδο. Όταν η είσοδος είναι 0, η έξοδος είναι 1. Όταν η είσοδος είναι 1, η έξοδος είναι 0. Η πύλη NOT κάνει ένα είδος αντιστροφής. Η μεταβλητή εξόδου είναι ίδια με τη μεταβλητή εισόδου, αλλά με μια ράβδο (υπεργραμμωμένη). Ο πίνακας ΟΧΙ αλήθειας με 1 και 0 είναι ο ίδιος με την προηγούμενη διάταξη αληθές/λάθος Ή αλήθεια (πίνακας).
Η εξίσωση ΔΕΝ είναι:
A = Q
Όπου Q = A και η μπάρα πάνω από το A εδώ σημαίνει συμπλήρωμα. Το συμπλήρωμα του 0 είναι 1 και το συμπλήρωμα του 1 είναι 0. Η πύλη NOT είναι επίσης γνωστή ως ΑΝΤΙΣΤΡΟΦΗ πύλη.
Αυτοί είναι οι θεμελιώδεις (ή ριζικοί) πίνακες αλήθειας και οι πύλες τους (μικρά κυκλώματα) στην ψηφιακή ηλεκτρονική (με άλγεβρα Boole). Οι άλλοι τρεις πίνακες αλήθειας που δίνονται στην παρακάτω εικόνα και οι πύλες τους είναι για λόγους ευκολίας και βασίζονται στους τρεις προηγούμενους πίνακες αλήθειας.
Υπάρχει ένας πίνακας και μια πύλη αλήθειας που προέρχονται από τον πίνακα και την πύλη αλήθειας ΚΑΙ. Ονομάζονται NAND (για NOT AND) πίνακας αλήθειας και η αντίστοιχη πύλη NAND. Ο πίνακας αλήθειας NAND και η πύλη NAND του είναι:
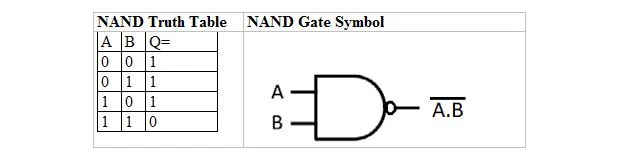
Για να λάβετε τον πίνακα αλήθειας NAND, μεταβείτε στην έξοδο του πίνακα αλήθειας AND και αντικαταστήστε κάθε ψηφίο με το συμπλήρωμά του. Το συμπλήρωμα του 0 είναι 1 και το συμπλήρωμα του 1 είναι 0. Η πύλη NAND είναι σαν την πύλη AND, αλλά έχει έναν μικρό κύκλο πριν από τη γραμμή εξόδου. Η εξίσωση NAND είναι:
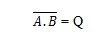
Όπου σημαίνει το συμπλήρωμα του αποτελέσματος των «Α» ΚΑΙ «Β». Η μπάρα (over-line) αντιπροσωπεύεται στην πύλη με τον μικρό κύκλο. Σημειώστε ότι η τελεία μεταξύ Α και Β μπορεί να παραλειφθεί.
Υπάρχει ένας άλλος πίνακας αλήθειας και πύλη που προέρχονται από τον πίνακα και την πύλη αλήθειας OR. Ονομάζονται NOR (για NOT OR) πίνακας αλήθειας και η αντίστοιχη πύλη NOR. Ο πίνακας αλήθειας NOR και η πύλη του NOR είναι:
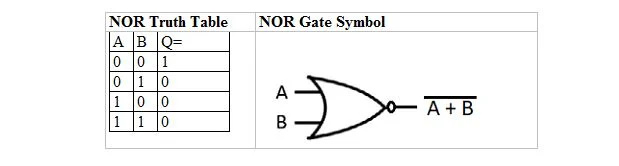
Για να λάβετε τον πίνακα αλήθειας NOR, μεταβείτε στην έξοδο του πίνακα αλήθειας OR και αντικαταστήστε κάθε ψηφίο με το συμπλήρωμά του. Το συμπλήρωμα του 0 είναι 1 και το συμπλήρωμα του 1 είναι 0. Η πύλη NOR είναι σαν την πύλη OR, αλλά έχει έναν μικρό κύκλο πριν από τη γραμμή εξόδου. Η εξίσωση NOR είναι:
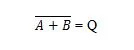
Οπου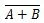 
σημαίνει το συμπλήρωμα του αποτελέσματος του «Α» Ή «Β». Η μπάρα (overline) αντιπροσωπεύεται στην πύλη με τον μικρό κύκλο.
Αποκλειστικό OR (XOR)
Ο πίνακας αλήθειας για την πύλη OR είναι:
Στα κανονικά αγγλικά, δεν είναι ξεκάθαρο αν η τελευταία σειρά του 1 Ή 1 θα πρέπει να δίνει 1 ή 0. Έτσι, στην άλγεβρα Boole, υπάρχουν δύο είδη πινάκων αλήθειας OR και δύο αντίστοιχες πύλες. Με το κανονικό OR, η τελευταία σειρά του 1 Ή 1 δίνει 1. Ο άλλος τύπος OR είναι το αποκλειστικό-OR (XOR) όπου οι τρεις πρώτες σειρές είναι ίδιες με τις τρεις πρώτες σειρές του κανονικού OR (συμπεριλαμβανομένης της εξόδου). Ωστόσο, για την τέταρτη και τελευταία σειρά, 1 Ή 1 δίνει 0.
Ο παρακάτω πίνακας δίνει τον πίνακα αλήθειας XOR και το σύμβολο της πύλης XOR (μικρό κύκλωμα):
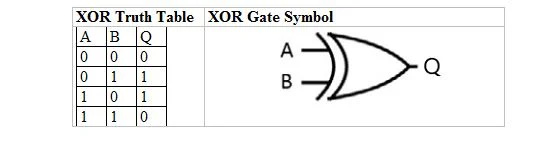
Τόσο για τον πίνακα αλήθειας XOR όσο και για την πύλη του, το 'A' όσο και το 'B' είναι δύο μεταβλητές εισόδου. Το 'Q' είναι η μεταβλητή εξόδου.
Η εξίσωση XOR είναι:
A ⊕ B = Q
Όπου το ⊕ εδώ σημαίνει Boolean XOR.
Το κανονικό Ή σημαίνει ένα ή και τα δύο. Αποκλειστικό Ή σημαίνει αυστηρά είτε και όχι και τα δύο.
2.3 Βουλικές αξιώσεις
Τα αξιώματα είναι υποθέσεις βάσει των οποίων εξάγονται ορισμένα συμπεράσματα. Υπάρχουν δέκα Boolean αξιώματα που έχουν τις ρίζες τους από τις εξισώσεις AND, OR και NOT (πίνακες αλήθειας). Αυτές οι εξισώσεις ονομάζονται επίσης συναρτήσεις. Οι θεμελιώδεις συναρτήσεις αντιγράφονται ως εξής:
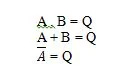
Αυτές είναι οι θεμελιώδεις συναρτήσεις (εξισώσεις) στην άλγεβρα Boole. Οι ακόλουθες τρεις εξισώσεις (συναρτήσεις) δεν είναι θεμελιώδεις συναρτήσεις:
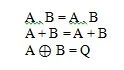
Αν και η τελευταία συνάρτηση εδώ είναι περίεργη, δεν θεωρείται θεμελιώδης συνάρτηση.
Τα αξιώματα Boolean είναι τα εξής:
Από τη λειτουργία ΚΑΙ
1) 0 . 0 = 0
είκοσι . 1 = 0
3) 1. 0 = 0
4) 1. 1 = 1
Από τη λειτουργία Ή
5) 0 + 0 = 0
6) 0 + 1 = 1
7) 1 + 0 = 1
8) 1 + 1 = 1
Από τη λειτουργία NOT
9) 0 = 1
10) 1 = 0
Σημείωση: Αυτά τα αξιώματα είναι απλώς οι γραμμές στους πίνακες αλήθειας ΚΑΙ, Ή, και ΟΧΙ που εκφράζονται με ανεξάρτητο τρόπο. Ο αναγνώστης θα πρέπει να απομνημονεύσει τα δεδομένα αξιώματα.
2.4 Ιδιότητες Boolean
Μια ιδιότητα είναι σαν χαρακτηριστικό κάτι. Οι ιδιότητες Boole είναι εξισώσεις που προέρχονται από τα δυαδικά αξιώματα. Σε αυτή την ενότητα, οι ιδιότητες δίδονται απλώς χωρίς τις παραγώγους τους και στη συνέχεια χρησιμοποιούνται στη συνέχεια. Υπάρχουν είκοσι πέντε από τα ακίνητα που ομαδοποιούνται σε δέκα επικεφαλίδες ως εξής:
Ιδιότητες της συνάρτησης AND
Ιδιοκτησία 1:
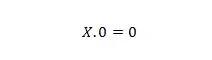
Όπου το X μπορεί να είναι 1 ή 0. Αυτό σημαίνει ότι ανεξάρτητα από το X, το αποτέλεσμα είναι πάντα 0.
Σημείωση: Μια μεταβλητή δεν πρέπει απαραίτητα να είναι A ή B ή C ή D. Μια μεταβλητή μπορεί να είναι W ή X ή Y ή Z ή οποιοδήποτε άλλο γράμμα.
Ιδιοκτησία 2:
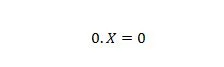
Όπου το X μπορεί να είναι 1 ή 0. Σημειώστε ότι η διαφορά μεταξύ της ιδιότητας 1 και της ιδιότητας 2 είναι ότι στην αριστερή πλευρά του πρόσημου ίσου και των δύο εξισώσεων, οι θέσεις των Χ και 0 ανταλλάσσονται.
Ιδιότητα 3:
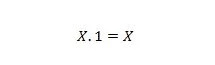
Αν το Χ είναι 0, τότε 0. 1 = 0. Εάν το Χ είναι 1, τότε 1. 1 = 1.
Ιδιοκτησία 4:
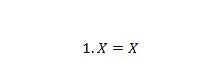
Αν το Χ είναι 0, τότε 1. 0 = 0. Εάν το Χ είναι 1, τότε 1. 1 = 1. Σημειώστε ότι η διαφορά μεταξύ της ιδιότητας 3 και της ιδιότητας 4 είναι ότι στην αριστερή πλευρά και των δύο εξισώσεων, οι θέσεις του Το X και το 1 εναλλάσσονται.
Ιδιότητες της συνάρτησης OR
Ιδιοκτησία 5:
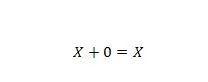
Όπου το Χ μπορεί να είναι 1 ή 0. Αυτό σημαίνει ότι αν το Χ είναι 0, το αποτέλεσμα είναι 0. Εάν το Χ είναι 1, το αποτέλεσμα είναι 1.
Ιδιοκτησία 6:
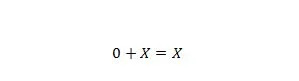
Όπου το X μπορεί να είναι 1 ή 0. Σημειώστε ότι η διαφορά μεταξύ της ιδιότητας 5 και της ιδιότητας 6 είναι ότι στην αριστερή πλευρά και των δύο εξισώσεων, οι θέσεις των Χ και 0 εναλλάσσονται.
Ιδιοκτησία 7:
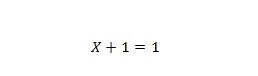
Εάν το Χ είναι 0, τότε 0 + 1 = 1. Εάν το Χ είναι 1, τότε 1 + 1 = 1.
Ιδιοκτησία 8:
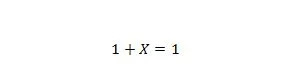
Εάν το X είναι 0, τότε 1 + 0 = 1. Εάν το Χ είναι 1, τότε 1 + 1 = 1. Σημειώστε ότι η διαφορά μεταξύ της ιδιότητας 7 και της ιδιότητας 8 είναι ότι στην αριστερή πλευρά και των δύο εξισώσεων, οι θέσεις του Το X και το 1 εναλλάσσονται.
Ιδιότητες που αφορούν το συνδυασμό μιας μεταβλητής με τον εαυτό της ή το συμπλήρωμά της
Ιδιοκτησία 9: 
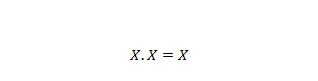
Δηλαδή: αν το Χ είναι 0, τότε 0 . 0 = 0. Αν το Χ είναι 1, τότε 1 . 1 = 1.
Ιδιοκτησία 10:
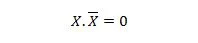
Δηλαδή: αν το Χ είναι 0, τότε 0. 1 = 0. Αν το Χ είναι 1, τότε 1. 0 = 0.
Για διαδοχικές μεταβλητές, αυτή η ιδιότητα γίνεται:
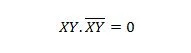
Ιδιοκτησία 11:
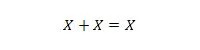
Δηλαδή: αν το Χ είναι 0, τότε 0 + 0 = 0. Εάν το Χ είναι 1, τότε 1 + 1 = 1 (από το κανονικό OR).
Ιδιοκτησία 12:
Δηλαδή: αν το Χ είναι 0, τότε 0 + 1 = 1. Αν Χ = 1, τότε 1 + 0 = 1.
Δηλαδή: αν το Χ είναι 0, τότε 0 + 1 = 1. Αν Χ = 1, τότε 1 + 0 = 1.
Διπλή Συμπλήρωση
Ιδιοκτησία 13:
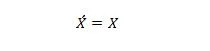
Όταν το Χ στην αριστερή πλευρά είναι 0, το Χ στη δεξιά πλευρά γίνεται 0. Όταν το Χ στη δεξιά πλευρά είναι 1, το Χ στην αριστερή πλευρά γίνεται 1. Με άλλα λόγια, διπλά συμπληρώματα δίνει πίσω την αρχική τιμή.
Ανταλλακτικό Δίκαιο
Ακίνητο 14:
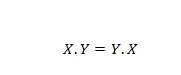
Αυτό σημαίνει ότι η εναλλαγή του πρώτου και του δεύτερου τελεστή για τον τελεστή AND, στην αριστερή πλευρά του πρόσημου ίσου, δεν έχει σημασία. η απάντηση παραμένει η ίδια αφού έχει γίνει η εναλλαγή στην αριστερή πλευρά. Αυτή η εξίσωση μπορεί να γραφτεί με τις τελείες να παραλείπονται ως: XY = YX.
Ακίνητο 15:
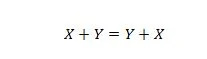
Η εξήγηση εδώ είναι η ίδια με την προηγούμενη AND, αλλά είναι για τον τελεστή OR.
Διανεμητικό Δίκαιο
Ακίνητο 16:
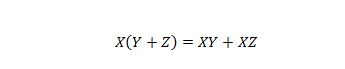
Εδώ υπάρχουν τρεις μεταβλητές: X, Y και Z. Κάθε μεταβλητή μπορεί να είναι είτε 1 είτε 0. Στην αριστερή πλευρά του συμβόλου ίσου, οι αγκύλες σημαίνουν να αξιολογήσουν πρώτα τι υπάρχει σε αυτές. Τότε, AND είναι το αποτέλεσμα με το X. Η δεξιά πλευρά λέει ότι τα Χ ΚΑΙ Υ μαζί, Ή τα Χ ΚΑΙ Ζ μαζί, είναι ίδια με την αριστερή πλευρά. Σημειώστε ότι ο τελεστής κουκκίδας για τα AND παραλείπεται σε όλη τη διάρκεια. και οι ενωμένες μεταβλητές εξακολουθούν να σημαίνουν ΚΑΙ.
Ακίνητο 17:
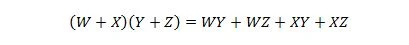
Αυτή η ιδιότητα είναι μια επέκταση της ιδιότητας 16 με την προστιθέμενη μεταβλητή του W.
Συνεταιριστικό Δίκαιο
Ακίνητο 18:
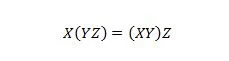
Οι αγκύλες σημαίνουν να αξιολογήσετε πρώτα τι υπάρχει στις αγκύλες. Έτσι, για την έκφραση στην αριστερή πλευρά, εάν το Y με το Z είναι AND πρώτα και το X είναι AND με το αποτέλεσμα, τότε αυτό το τελικό αποτέλεσμα στην αριστερή πλευρά είναι το ίδιο με το τελικό αποτέλεσμα στη δεξιά -το χέρι όπου το Χ με το Υ είναι AND πρώτα πριν AND το αποτέλεσμα με το Ζ. Σημειώστε ότι οι τελείες έχουν παραλειφθεί στην εξίσωση.
Ακίνητο 19:
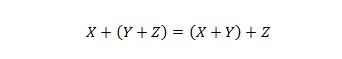
Αυτή η ιδιότητα εξηγείται με παρόμοιο τρόπο όπως η ιδιότητα 18, αλλά ο τελεστής OR χρησιμοποιείται αντί για τον τελεστή AND. Ο τελεστής OR + δεν παραλείπεται ποτέ από μια Boolean έκφραση για λόγους απλότητας. Από την άλλη πλευρά, ο τελεστής AND μπορεί να παραλειφθεί και οι δύο μεταβλητές μπορούν να ενωθούν.
Απορρόφηση
Ιδιοκτησία 20:
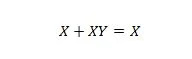
Με αυτήν την εξίσωση, ανεξάρτητα από το τι είναι το Y, η δεξιά πλευρά θα είναι πάντα Χ (απορροφημένη).
Ακίνητο 21:
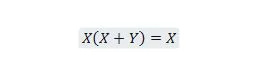
Επίσης, με αυτήν την εξίσωση, ανεξάρτητα από το τι είναι το Y, η δεξιά πλευρά θα είναι πάντα Χ (απορροφημένη). Αυτή η ιδιότητα 21 είναι ίδια με την ιδιότητα 20 που είναι:
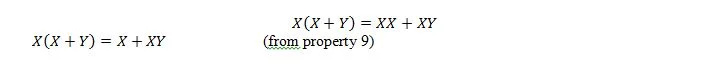
Εδώ, χρησιμοποιούμε τον διανεμητικό νόμο και το γεγονός ότι X.X = X της ιδιότητας 9.
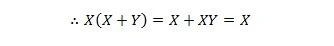
Μια Ταυτότητα
Ακίνητο 22:
Αυτό σημαίνει ότι για την έκφραση X + Y, το συμπλήρωμα του X μπροστά από το Y δεν αλλάζει την έκφραση.
Ακίνητο 23:
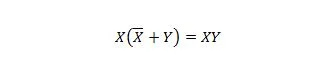
Αυτό σημαίνει ότι για την έκφραση XY, το συμπλήρωμα του X ORed με το Y σε αγκύλες, που γίνεται πρώτα, δεν αλλάζει την έκφραση XY.
Νόμος του DeMorgan
Ακίνητο 24:
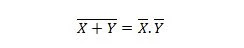
Αυτό σημαίνει ότι μια πύλη NOR (NOT OR) έχει το ίδιο αποτέλεσμα με το NOT των δύο εισόδων πριν από την AND τους.
Ακίνητο 25:
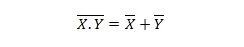
Αυτό σημαίνει ότι μια πύλη NAND (NOT AND) έχει το ίδιο αποτέλεσμα με το NOT των δύο εισόδων πριν από το OR.
Οι παρεχόμενες εικόνες είναι οι 25 ιδιότητες. Μπορούν να αποδειχθούν αντικαθιστώντας όλες τις διαφορετικές πιθανές τιμές του 1 και του 0, σε κάθε έκφραση στην αριστερή πλευρά, για να δούμε αν λαμβάνεται η έκφραση (ή το αποτέλεσμα) στη δεξιά πλευρά. Οι αποδείξεις αφήνονται ως άσκηση για τον αναγνώστη.
2.5 Απλοποίηση σύνθετων εκφράσεων
Οι ακόλουθες δύο λειτουργίες είναι ίδιες:
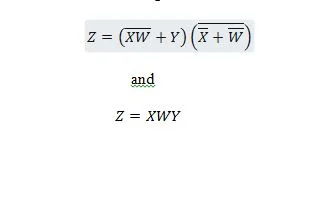
Z είναι η έξοδος και X, W και Y είναι οι είσοδοι. Το πρώτο χρειάζεται μια πύλη NAND, μια πύλη OR, μια πύλη AND, δύο πύλες NOT, μια πύλη OR και μια πύλη NOR. Το δεύτερο χρειάζεται μόνο δύο ΚΑΙ πύλες. Η πρώτη είναι μια εξίσωση με μια σύνθετη έκφραση, στη δεξιά πλευρά, η οποία έχει απλοποιηθεί (ανάγεται) στον μονό όρο της δεξιάς έκφρασης για τη δεύτερη εξίσωση.
Η απλοποίηση ή η μείωση οδηγεί σε μικρότερο αριθμό πυλών προκειμένου να υλοποιηθεί η ίδια λειτουργία με ένα κύκλωμα. Ένα τόσο μικρότερο κύκλωμα μπορεί να είναι μέρος ενός ολοκληρωμένου κυκλώματος (IC) ή να είναι αυτόνομο κύκλωμα στην επιφάνεια της μητρικής πλακέτας του υπολογιστή.
Όταν μια συνάρτηση (εξίσωση) φτάσει στη διαδικασία σχεδιασμού, πρέπει να γίνει απλοποίηση για να μειωθεί ο αριθμός των πυλών και να καταλήξουμε σε ένα φθηνότερο κύκλωμα. Η απλούστευση απαιτεί τη χρήση μιας ή περισσότερων από τις προηγούμενες είκοσι πέντε ιδιότητες Boolean.
Παράδειγμα 2.51:
Μειώστε την εξίσωση:
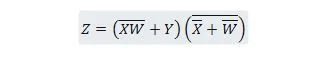
Σημείωση: Δύο παρενθέσεις η μία δίπλα στην άλλη σημαίνει ότι οι παρενθέσεις είναι AND (η κουκκίδα μεταξύ τους προαιρετικά δεν έχει γραφτεί).
Λύση:
Για τις λύσεις, η αιτιολόγηση (λόγος) για κάθε βήμα δίνεται στα δεξιά του βήματος, μέσα σε αγκύλες. Ο αναγνώστης πρέπει να διαβάσει κάθε βήμα και την αιτιολόγησή του. Ο αναγνώστης θα πρέπει επίσης να αναφέρεται στις προηγούμενες ιδιότητες καθώς διαβάζει τα βήματα μείωσης συναρτήσεων.
Παράδειγμα 2.52:
Απλοποιώ:
2.6 Ελάχιστο άθροισμα προϊόντων
Οι ακόλουθες δύο λειτουργίες είναι ίδιες:
Και οι δύο δεξιές εκφράσεις και των δύο εξισώσεων λέγεται ότι έχουν τη μορφή αθροίσματος προϊόντων (SP). Μια ρητή έκφραση λέγεται ότι έχει τη μορφή Sum of Product, εάν δεν έχει παρενθέσεις. Είναι προφανές ότι η πρώτη συνάρτηση (εξίσωση) χρειάζεται περισσότερες πύλες από τη δεύτερη συνάρτηση.
Η πρώτη δεξιά έκφραση μπορεί ακόμα να μειωθεί για να ληφθεί η δεύτερη συνάρτηση. Η δεύτερη έκφραση στη δεξιά πλευρά δεν μπορεί να απλοποιηθεί περαιτέρω και εξακολουθεί να εκφράζεται ως Άθροισμα προϊόντων («προσθήκη» όρων). Η δεύτερη έκφραση της δεξιάς πλευράς δεν μπορεί πραγματικά να απλοποιηθεί περαιτέρω. Έτσι, λέγεται ότι είναι στη μορφή Ελάχιστου Αθροίσματος Προϊόντων (MSP).
Παράδειγμα 2.61:
Φέρτε την παρακάτω συνάρτηση πρώτα στη φόρμα Sum of Products και μετά στη φόρμα Minimum Sum of Products.
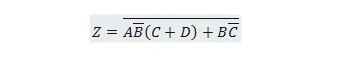
Λύση:
Κατά την επίλυση προβλημάτων όπως αυτό, μία ή περισσότερες από τις προηγούμενες είκοσι πέντε ιδιότητες πρέπει να χρησιμοποιηθούν όπως απεικονίζεται σε αυτήν τη λύση:
2.6 Ελάχιστο άθροισμα προϊόντων
Οι ακόλουθες δύο λειτουργίες είναι ίδιες:
Και οι δύο δεξιές εκφράσεις και των δύο εξισώσεων λέγεται ότι έχουν τη μορφή αθροίσματος προϊόντων (SP). Μια ρητή έκφραση λέγεται ότι έχει τη μορφή Sum of Product, εάν δεν έχει παρενθέσεις. Είναι προφανές ότι η πρώτη συνάρτηση (εξίσωση) χρειάζεται περισσότερες πύλες από τη δεύτερη συνάρτηση.
Η πρώτη δεξιά έκφραση μπορεί ακόμα να μειωθεί για να ληφθεί η δεύτερη συνάρτηση. Η δεύτερη έκφραση στη δεξιά πλευρά δεν μπορεί να απλοποιηθεί περαιτέρω και εξακολουθεί να εκφράζεται ως Άθροισμα προϊόντων («προσθήκη» όρων). Η δεύτερη έκφραση της δεξιάς πλευράς δεν μπορεί πραγματικά να απλοποιηθεί περαιτέρω. Έτσι, λέγεται ότι είναι στη μορφή Ελάχιστου Αθροίσματος Προϊόντων (MSP).
Παράδειγμα 2.61:
Φέρτε την παρακάτω συνάρτηση πρώτα στη φόρμα Sum of Products και μετά στη φόρμα Minimum Sum of Products.
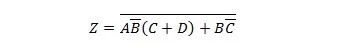
Λύση:
Κατά την επίλυση προβλημάτων όπως αυτό, μία ή περισσότερες από τις προηγούμενες είκοσι πέντε ιδιότητες πρέπει να χρησιμοποιηθούν όπως απεικονίζεται σε αυτήν τη λύση:
Αυτή η τελευταία έκφραση είναι στη μορφή Sum of Products (SP), αλλά όχι στη μορφή Minimum Sum of Products (MSP). Το πρώτο μέρος της ερώτησης έχει απαντηθεί. Η λύση για το δεύτερο μέρος είναι η εξής:
Αυτή η τελευταία απλοποιημένη συνάρτηση (εξίσωση) είναι σε μορφή MSP και χρειάζεται λιγότερο αριθμό πυλών για υλοποίηση από την αντίστοιχη μορφή SP της. Θυμηθείτε: SP σημαίνει άθροισμα προϊόντων ενώ MSP σημαίνει Ελάχιστο άθροισμα προϊόντων.
Παράδειγμα 2.62:
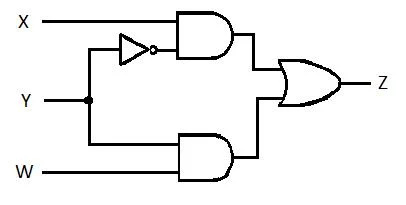
Το παρακάτω κύκλωμα έχει τις εισόδους X, Y και W και το Z είναι η έξοδος. Δημιουργήστε τη συνάρτηση αθροίσματος προϊόντων (SP) (φαινομενική συνάρτηση ελάχιστου αθροίσματος προϊόντων) για το Z. Στη συνέχεια, δημιουργήστε το αληθινό πιο μειωμένο (ελαχιστοποιημένο) άθροισμα προϊόντων (MSP). Στη συνέχεια, εφαρμόστε το κύκλωμα MSP (σχεδιάστε το δίκτυο πύλης MSP).
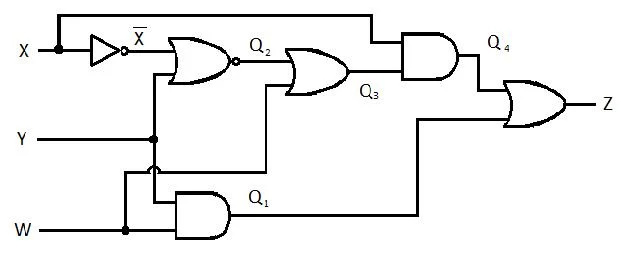
Εικ. 2.61 Ένα κύκλωμα πύλης
Λύση:
Πριν ξεκινήσει η διαδικασία απλοποίησης, η έκφραση για το Z πρέπει να ληφθεί ως X, Y και W. Ανατρέξτε σε αυτό το παράδειγμα απεικόνισης από το διάγραμμα:
Αυτή είναι η έκφραση του Z ως προς τα X, Y και W. Μετά από αυτό, μπορεί να γίνει η απλοποίηση σε προφανές MSP. Το προφανές MSP είναι SP.
Αυτή η τελευταία εξίσωση (συνάρτηση) είναι σε μορφή SP. Δεν είναι αλήθεια Ελάχιστο άθροισμα προϊόντων (δεν είναι ακόμη MSP). Επομένως, η μείωση (ελαχιστοποίηση) πρέπει να συνεχιστεί.
Αυτή η τελευταία εξίσωση (συνάρτηση) είναι ένα πραγματικό ελάχιστο άθροισμα προϊόντων (MSP). Και το κύκλωμα πύλης ελάχιστου αθροίσματος προϊόντων (πραγματική ελαχιστοποίηση) είναι:
Εικ. 2.62 Κύκλωμα πύλης MSP
Σχόλιο
Από την ανάλυση σε αυτήν την ενότητα, φαίνεται ότι δεν είναι σαφές εάν το Άθροισμα Προϊόντων είναι το Ελάχιστο Άθροισμα Προϊόντων ή όχι. Το SP δεν είναι πολύ χρήσιμο. Είναι το MSP που είναι πολύ χρήσιμο. Υπάρχει ένας σίγουρος τρόπος για να αποκτήσετε MSP. είναι να χρησιμοποιήσετε τον χάρτη Karnaugh. Ο χάρτης Karnaugh είναι πέρα από το πεδίο αυτού του διαδικτυακού μαθήματος καριέρας.
2.7 Προβλήματα
Συνιστάται στον αναγνώστη να λύσει όλα τα προβλήματα σε ένα κεφάλαιο πριν προχωρήσει στο επόμενο κεφάλαιο.
- Δημιουργήστε τους πίνακες AND, OR και NOT με τις αντίστοιχες πύλες τους.
- Καταγράψτε τα δέκα Boolean Postulates στις διαφορετικές κατηγορίες τους, ονομάζοντας τις κατηγορίες.
- Χωρίς εξήγηση, γράψτε τις είκοσι έξι ιδιότητες της άλγεβρας Boole στις διαφορετικές κατηγορίες τους, ονομάζοντας τις κατηγορίες.
- Μειώστε την εξίσωση χρησιμοποιώντας τις ιδιότητες Boolean και παραθέτοντας τις κατηγορίες που χρησιμοποιούνται.
- Μειώστε την εξίσωση χρησιμοποιώντας τις ιδιότητες Boolean και παραθέτοντας τις κατηγορίες που χρησιμοποιούνται.
- Χρησιμοποιώντας τις ιδιότητες Boolean και παραθέτοντας τις κατηγορίες που χρησιμοποιούνται, μειώστε την ακόλουθη εξίσωση - πρώτα σε Άθροισμα προϊόντων και μετά σε Ελάχιστο άθροισμα προϊόντων:
- Χρησιμοποιώντας τις ιδιότητες Boolean και παραθέτοντας τις κατηγορίες που χρησιμοποιούνται, μειώστε την ακόλουθη εξίσωση - πρώτα σε Άθροισμα προϊόντων και μετά σε Ελάχιστο άθροισμα προϊόντων:
